뉴스
"수의"(으)로 총 857건 검색되었습니다.
- "니코틴 중독, 뇌 자기자극으로 치료 가능"연합뉴스 2023.09.25
- 두 가지 형태가 있다. cTBS는 3번의 돌발 자극을 40초 동안 연속적으로 반복하고 iTBS는 같은 수의 돌발 펄스를 190초 이상에 걸쳐 불규칙적으로 발사한다. 연구팀은 억제 제어(IC)에 관여하는 뇌 부위인 우반구 하전두(right inferior frontal gyrus)에 cTBS와 iTBS가 어떤 영향을 미치는지를 실험해 봤다. 그 ... ...

- 적은 데이터 학습해도 신약 후보 내놓는 생성형 AI동아사이언스 2023.09.19
- 연구팀이 개발한 AI 모델이 제시한 분자 구조를 분석한 결과, 약물 후보로 예측된 다수의 생성물이 기존 데이터에 있는 분자와는 유사성이 낮은 신규 구조임이 확인됐다. 다양한 신규 약물 후보 화합물을 생성해내는 데 성공한 것이다. 남호정 교수는 “신약 개발 초기 단계에 적용해 후보물질 ... ...
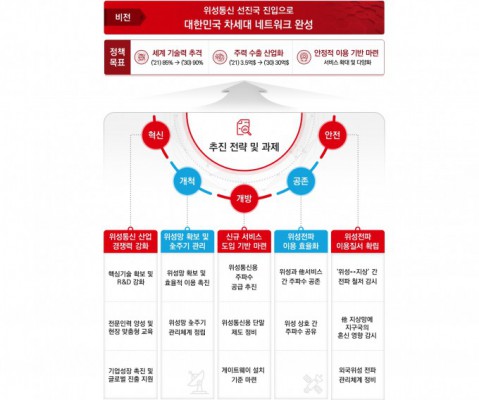
- 저궤도 위성통신망 구축에 5년간 4800억 투입동아사이언스 2023.09.18
- 독점되지 않고 후발 위성사업자 진입과 위성사업자 상호 간 공존이 보장되도록 위성주파수의 ‘사용 신청 → 상호 협의・조정 → 운용 조건 부과’의 절차를 제도화하는 것을 검토한다. 필요시 위성사업자에 대한 주파수 사용을 승인할 때 향후 후발사업자와 협의・조정에 성실히 응하도록 의무를 ... ...

- 우주방사선 환경 구현해 위성에 쓰일 반도체 성능 시험동아사이언스 2023.09.12
- 연구원이 보유한 국내 하나뿐인 선형 대용량 양성자가속기는 1초당 1.2경이라는 엄청난 수의 양성자를 조사할 수 있다. 특히 입자 방사선의 일종인 양성자 방사선은 위성 궤도 기준으로 우주 방사선의 약 85%를 차지하기 때문에 양성자 빔 조사를 통해 우주·항공용 반도체를 사전 검증하는 것이 ... ...

- "반도체·양자·우주도 R&D예산 삭감 칼날 못피했다"동아사이언스 2023.09.04
- 설치한 '소부장 특별회계'와 2050 탄소중립 달성을 위해 설치한 '기후대응기금'은 총 사업수의 약 90%가 삭감됐다. 삭감 규모별로 살펴보면 취약계층에 대한 정보통신 보조기기 보급 및 정보접근성 제고를 위한 '디지털 격차 해소 기반 조성' 사업이 823억원으로 가장 많은 예산이 삭감됐다. ... ...

- [주말N수학] 2022 필즈상 영광의 순간 이후…수학자의 도전은 계속된다수학동아 2023.09.02
- “자신과 1로만 나눠질 수 있는 소수는 정수론에서 ‘원자’로 비유된다”면서 소수의 매력을 강조했습니다. 또한 자신이 왜 소수 연구를 시작하게 됐는지 필즈상을 받았다는 소식을 들었을 때 제일 먼저 든 생각이 무엇인지에 대해서도 이야기했습니다. 마지막으로 “나는 아직 수학에서 내 ... ...

- 코로나19 재유행 열쇠 '사슴'...변이속도, 사람보다 3배 빨라동아사이언스 2023.09.01
- 통해 유행할 가능성이 있다는 우려가 제기된다. 앤드루 보우먼 미국 오하이오주립대 수의학·예방의학과 교수 연구팀은 흰꼬리사슴을 대상으로 코로나19 감염과 변이 양상을 연구한 결과를 국제학술지 '네이처 커뮤니케이션즈'에 지난달 28일(현지시간) 공개했다. 연구팀은 2021년 11월부터 202 ... ...

- 물리학 '매직넘버' 이론 뒤흔든 산소 동위원소 발견동아사이언스 2023.08.31
- 0일(현지시간) 국제학술지 '네이처'에 발표했다. 앞서 과학자들은 원자핵 안에 일정한 수의 양성자나 중성자를 가진 원소에 주목했다. 이론상 양성자나 중성자가 특정 개수만 존재할 때 원자핵은 훨씬 안정적이기 때문이다. 반감기가 긴 안정적인 상태를 이룰 수 있는 양성자나 중성자의 수는 ... ...

- [주말N수학] 대수와 기하는 어떤 관계일까수학동아 2023.07.22
- 포물선, 원과 연결돼서 기하학과 대수학을 확실히 통합하는 거지요." Q(인문학자). 변수의 개수가 많아질수록 복잡한 형태의 도형이 만들어지겠네요. A(수학자). "네, 정확합니다. 보통 데카르트의 좌표평면처럼 x축, y축을 가진 2차원을 생각하는데요. 변수를 늘리지 말라는 법이 없잖아요. 예를 ... ...
- [日 오염수 팩트체크] ⑥삼중수소가 몸 속에서 암을 유발한다?과학동아 2023.07.14
- 남는 삼중수소의 양은 극히 적다. 2011년 캐나다원자력안전위원회가 ICRP의 ‘삼중수소수의 생물역학’ 자료를 인용해 발표한 바에 따르면 우리 몸에 삼중수소가 들어와 존재할 수 있는 형태의 97%는 HTO다. 나머지 3%는 반감기가 약 40일인 OBT와 반감기가 350일인 OBT다. 몸속 삼중수소는 거의 물의 ... ...








