뉴스
"사면"(으)로 총 97건 검색되었습니다.
- [박진영의 사회심리학] 받는 기쁨보다 주는 기쁨이 더 오래간다2018.12.22
- 위해서 살 때보다 더 이 사람이 무엇을 좋아할지, 무엇을 필요로 할지, 이걸 사면 또 저걸 사면 반응이 어떨지 등 더 다양한 생각을 하게 된다. 사고 난 후에도 더 오랫동안 두근두근 하기도 한다. ‘예측 불가능’한 고통이 더 오래 가듯 예측 불가능한 기쁨 역시 더 오래 가는 법이다. 또한 여행도 ... ...
- [뉴스룸]과학기술계까지 정치색 오해 사면 안 된다동아사이언스 l2018.12.17
- 정부는 아니라고 하지만 국내 과학기술계는 끓고 있다. 신성철 KAIST 총장 고발 얘기다. 고발부터 총장 직무정지 추진까지 지나치게 서두르는 정부 대응에 자세한 내막을 모르겠다는 과학자들도 “지나치게 몰아치는 것 같다”고 했다. 과학기술계 기관장 물갈이가 다시 이어지는 거냐고도 했다. ... ...
- [내 마음은 왜 이럴까?] 결백한 자의 죄책감2018.12.02
- 요청했다. 이후 10년이 지난 2017년이 되어서야 주지사는 노퍽의 네 남자에게 무조건 사면을 명령했다. 사진출처 : https://www.navytimes.com/news/your-navy/2018/04/03/virginia-governor-oks-paying-norfolk-four-35m/ 귀인 이론(attributional theory)에 의하면, 수치심은 이상적인 자신의 표상과 불일치하는 일을 겪을 때 그리고 ... ...
- [내 마음 왜 이럴까?] 규율과 복종으로 스스로 옥죄는 삶...강박성의 진화 2018.08.19
- 지키는 사람이 있다는 것은 다행스러운 일입니다. 옛날에는 숙지황을 사면 보통의 것은 얼마, 그보다 나은 것은 얼마의 값으로 구별했고, 구증구포(九蒸九暴)한 것은 3배 이상 비쌌다. 구증구포란, 찌고 말리기를 아홉 번 한 것이다. 말을 믿고 사는 것이다. 신용이다. 지금은 그런 말조차 ... ...
- [짬짜면 과학 교실]작은 생물들의 큰 세계2018.08.11
- 적절한 환경이 되면 짧은 시간에 많은 수로 늘어나요. 그래서 여름철에 김밥을 사면 얼마 안 가서 상할 수 있으니 가급적 빨리 먹어야 해요. GiB 제공 해로운 세균이 우리 몸속에 들어오더라도 그 수가 아주 적으면 우리 몸이 견뎌내지만, 많은 수가 몸속에 들어오면 유익한 균이 모두 무찌를 수 ... ...
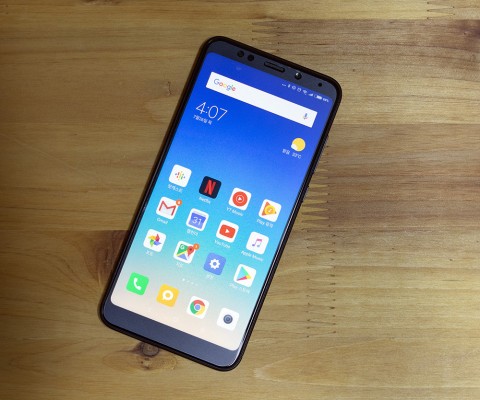
- [써보니] 싼 가격에 가려진 '샤오미 홍미5' 의 놀라운 매력들2018.07.27
- 부담없이 구입했다. 고장나면 어쩌냐는 주변의 걱정도 ‘반 값이니 고장나면 하나 더 사면 되지’라는 반쯤 농담 섞인 마음으로 대했다. 지금 반년을 돌아보고 남은 것은 샤오미의 제품에 대한 신뢰가 가장 크다. 이 보다 더 공들여서 만드는 플래그십은 어떤 경험을 줄까? 미8에 자꾸 눈이 가는 ... ...
- 음파 그대로 통과… ‘3D 음향투명망토’ 탄생동아사이언스 l2018.06.08
- 사면체 8개를 이어 붙인 팔각뿔 형태다. 너비는 1m, 높이는 0.6m 규모다. 각각의 사면체 하나당 92개의 직사각형 철 조각이 격자를 이루며 층층이 쌓인 형태다. 전체는 총 736개의 철 조각으로 이뤄져 있다. 이 조각들은 모두 살짝 고정돼 있을 뿐 물이 자유자재로 드나들 수 있도록 설계됐기 때문에 ... ...
- [강석기의 과학카페] 밀가루 글루텐 유해성, 여전히 논란 중2018.05.29
- 일어날 수 있다는 사실을 알게 됐다. 그 결과 40대 중반부터 실천하고 있는 ‘하나를 사면 하나를 버리는’ 방침에서 예외로 했던 책도 앞으로는 포함하기로 생각을 바꿨다. ‘책 저장장애’를 몰랐다면 글을 써서 먹고 사는 필자가 책을 버린다는 생각을 하기는 어려웠을 것이다. (관련기사 ... ...
- [강석기의 과학카페] 마음이 허(虛)하면 소유물에 집착한다2018.05.22
- 꺼내보지 않을 책들이 많은 게 사실이다. 이제 50이 됐으니 앞으로는 책도 ‘한 권을 사면 한 권을 버려야’겠다. 예전에 어떤 책인가 잡지에서 법정 스님의 방을 본 적이 있다. 몸 하나 누일 작은 공간에는 서안(書案)과 책 몇 권이 있을 뿐 가구도 벽을 장식한 그림도 없었다. 창호로 들어오는 ... ...
- [2018년 필즈상] 수학 영재에서 저차원 위상수학의 대가로! 수학자 치프리안 마놀레스쿠 교수 수학동아 l2018.04.05
- 점, 1차원 삼각형은 선, 2차원 삼각형은 우리가 생각하는 삼각형, 3차원 삼각형은 사면체를 말합니다. 1~3차원 다양체는 모두 삼각화가 가능하고, 4차원에서는 불가능한 예가 있다는 것이 알려져 있었습니다. 하지만 5차원 이상에 대해서는 미해결 난제였지요. 삼각화 추측을 곧바로 공략하는 게 ... ...
이전123456789 다음
