추천검색어 다음

뉴스

"다음다음"(으)로 총 6,319건 검색되었습니다.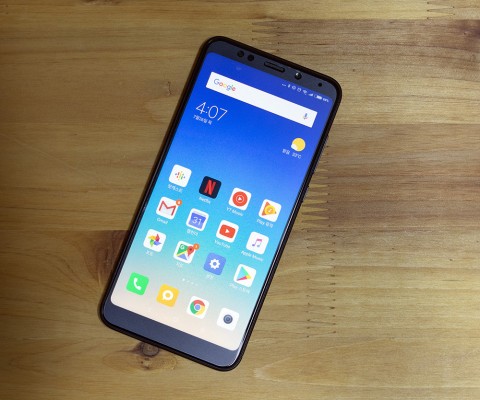

[써보니] 싼 가격에 가려진 '샤오미 홍미5' 의 놀라운 매력들2018.07.27

샤오미의 보급형 홍미 5 플러스를 반년째 쓰고 있다. 홍미 5 플러스는 5.99인치 디스플레이에 스냅드래곤 625 프로세서를 쓰는 중급기, 혹은 보급형 스마트폰에 들어간다. 지금까지 여러 부분에서 상당히 만족스럽게 쓰고 있는 제품이다.   최근 샤오미의 홍미 노트5 프로가 국내에 출시됐다. 정확히는 ... ...

목마른 ‘우주여행자’ 여기에서 물 한잔 하세요2018.07.27

화성 남극 지역의 지표를 덮은 물과 이산화탄소로 된 얼음(위)과, 그 부근에서 새롭게 발견된 지하 호수로 추정되는 지역(아래 레이더 영상). -사진 제공 INAF, USGS 태양계 끝을 향하는 우주선에 탑승했다. 예상치 못한 문제가 생겨 물을 외부에서 공급받아야 한다면 어떻게 해야 할까. 태양계를 여행하 ... ...

한국의 코워킹스페이스, “효용성 높고, 네트워킹에 아쉬워”2018.07.26

'코워킹 스페이스’, ‘공유 오피스’라는 단어가 점점 낯설지 않은 개념이 되고 있습니다. 코워킹 스페이스는 커다란 사무 공간을 여러 회사, 혹은 개인이 나누어 쓰는 환경을 말하지요. 애초 이 개념은 1994년 독일에서 시작됐는데, 썩 인기를 누리지 못하다가 세계적인 불황과 스타트업 붐과 함께 ... ...

15년 만에 지구 가까이 오는 화성…28일 새벽부터 우주쇼 펼쳐진다동아사이언스 l2018.07.24

‘가마솥 더위’가 연일 지속되는 가운데 이달 말에는 열대야로 잠 못 드는 밤을 우주쇼로 달래보면 어떨까.   24일 한국천문연구원에 따르면 오는 31일 화성이 2003년 이후 15년 만에 지구와 가장 가까운 지점에 놓인다. 이보다 사흘 앞선 28일에는 올 들어 두 번째 개기월식이 예정돼 있다. 28일 새벽 ... ...

[강석기의 과학카페] 고기를 향한 무서운 열망... 어떻게 해결할까? 2018.07.24

동물들은 인간이 그렇게 만들 때만 불행하다는 사실을 명심하라. - W. H. 허드슨   소는 여러 면에서 사람과 비슷한 욕구를 지녔다. 스트레스가 없어야 하고, 적당한 잠자리, 깨끗한 먹이와 물, 운동하거나 돌아다니거나 산책을 하거나 아니면 그냥 멍하니 서 있을 자유가 있어야 한다. - 로저먼드 영, ... ...

EU가 구글을 압박하는 세 가지 이슈바이라인 네트워크 l2018.07.24

EU가 지난 주 구글에 천문학적인 과징금을 부과했다. 무려 5조 7000억원 규모. 이는 1년 전 EU가 구글에 부과했던 사상 최대의 과징금 3조1000억원 기록을 다시 경신한 것이다. 이는 구글의 1분기 영업이익에 맞먹는 규모다. 아무리 돈많은 구글이라도 부담이 되지 않을 수 없는 금액이다. EU는 구글에 엄 ... ...

원자 3~4개 연결, 고효율 ‘미래형 촉매’ 만들었다동아사이언스 l2018.07.23

로듐 앙상블 촉매를 이용한 자동차 배기가스 정화 반응 개념도. KAIST 제공.   화학 산업계는 ‘촉매’를 놓고 전쟁을 벌이고 있다.   촉매는 각종 화학반응을 돕는 백금, 로듐 등 고가 물질이 많이 쓰인다. 화학제품을 만드는 과정에서 반응성이 뛰어난 촉매를 쓸수록 산업 효율 역시 높아진다. 배기 ... ...

[팔라우 힐링레터] 아빠의 육아 일기 '파이프 피쉬'2018.07.22

과거에 비해 요즘 사회의 가장 변화된 모습 중 하나는 아마도 남편이 육아에 참여하는 모습인 듯 싶다. 힘든 아내와 함께 하는 육아의 모습은 자식에 대한 사랑을 나타낼뿐 아니라 부부 서로 간 사랑도 돈독하게 해 주리라.      사랑 속에서 자라난 아이들은 더 아름다운 세상을 만들 것이다. 이 ... ...

[내 마음은 왜 이럴까?] 정신장애는 실재하는가?2018.07.22

정신장애는 단지 사회적으로 만들어진 신화라는 오랜 주장이 있습니다. 정신장애는 흔히 평소에 보인 이상한 말이나 행동과 같은 병력, 그리고 정신과 의사의 면담을 통해서 진단합니다. 그런데 평소에 보인 ‘이상한’ 언행이라는 말이 좀 ‘이상’하다는 주장이요. 그 ‘이상한’이라는 기준은 ... ...

[박진영의 사회심리학] 부모의 가혹한 양육이 자녀 비만 부른다2018.07.21

비만과 과체중에 대한 경고는 흔히 들을 수 있다. 그런데 무엇이 비만에 영향을 줄까? 먹는 것과 운동 외에도 어떤 환경적인 요소들을 조심해야 하는걸까?    GIB 제공     부모의 가혹한 양육 방식이 자녀 비만 불러온다 청소년 건강 저널(Journal of adolescent health)에 실린 브렌다 로만(Brenda Lohman) 등 ... ...

 이전384385386387388389390391392 다음