뉴스
"소수"(으)로 총 980건 검색되었습니다.

- [주말N수학] 수학자의 연구 여행기, 41년 역사의 군론학회 GSA수학동아 l2022.12.17
- PORC 추측은 1960년 영국 수학자 그레이엄 히그먼이 처음 제시한 추측으로, 임의의 소수 p와 자연수 n에 대해 원소의 개수가 p의 거듭제곱(pn)꼴인 p군의 분포를 예상한 추측입니다. 62년이 지난 지금도 여전히 풀리지 않은 군론의 오래된 난제예요. 저는 마이클 본-리 옥스퍼드대 명예교수님과 함께 ... ...

- 우주개발 화두는 '안보'와 '우주환경'...공론화 서둘러야동아사이언스 l2022.12.12
- 포럼’이 열렸다. 아부다비 스페이스 디베이트 포럼 제공. “우주는 이제 냉전시대 소수 강대국들이 펼치던 경쟁의 공간에서 전 세계 70여개국이 참여하는 다자간 공간으로 변모했다.” 지난 5~6일(현지시간) 아랍에미리트(UAE) 아부다비국영석유회사(ADNOC) 비즈니스센터에서 열린 ‘아부다비 ... ...

- [주말N수학] 필즈상 수상자도 놀랐다...정수론 난제 해결한 고3수학동아 l2022.12.03
- 가설’이 카마이클 수에도 적용될 거라고 추측했습니다. 2016년 메이나드 교수는 소수의 분포에 관한 논문을 발표했는데 라슨은 여기에 나온 방법을 활용해 자연수 X가 충분히 클 때 X와 2X 사이에 카마이클 수가 항상 존재하며, 최소 몇 개가 있는지 알 수 있는 수식을 알아냈습니다. 메이나드 교수는 ... ...

- [주말N수학] 단 한번의 기회가 수학자의 길로 인도수학동아 l2022.11.19
- 교수님은 아주 열정적으로 당시 교수님의 베스트셀러 도서인 '소수의 음악'에 담긴 소수 이야기를 재밌게 들려주셨고, 저는 강연에 감명받아 그 책을 사서 2일 동안 반복해서 읽었습니다. 그리고 그때 ‘저런 분 밑에서 수학을 배우고 싶다’는 마음이 들었습니다. 저는 이 강연을 통해 진정한 ... ...
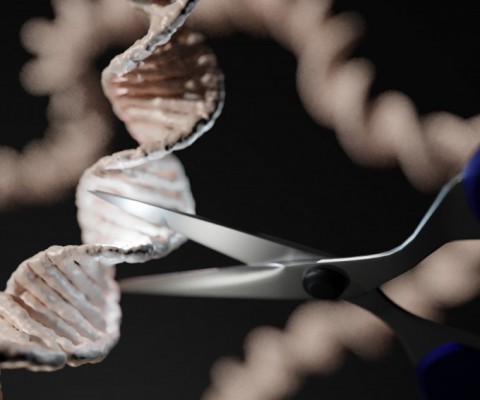
- 유전자가위로 암 치료 가능성 열려…미국 연구진 임상시험 성공동아사이언스 l2022.11.11
- 등에서 차이를 보인다. 연구팀은 “환자들 사이 일부 공유되는 돌연변이가 있지만 이는 소수로, 환자마다 대부분 다르다”며 “이 돌연변이를 타겟으로 한 환자 맞춤형 암 세포 파괴가 가능하다는 의미”라고 말했다. 연구팀은 임상 시험 참가자들에 조작된 T세포를 주입했다. 최대 3개의 서로 다른 ... ...

- 한국 반도체 위기론..."범국가 전략 필요"동아사이언스 l2022.10.28
- 0배가 넘고, 중국은 한국의 수십 배에 이르는 것으로 분석된다. 다만 국내 연구자들도 소수정예로 반도체 전쟁 무기를 준비해왔다. 김 소장은 “KIST 연구진과 이종호 과학기술정보통신부 장관, 최기영 서울대 교수 등은 2016년부터 차세대 AI 반도체로 꼽히는 뉴로모픽 기술 개발에 집중해왔다”며 ... ...

- [과기원은 지금] '2022 GIST 과학문화주간' 개최 外동아사이언스 l2022.10.27
- 재현하는 것이 가능하다. 이번에 개발된 나노 계면활성제는 ‘친수성을 띠는 머리’와 ‘소수성을 띠는 줄기’로 구성됐다. 이 같은 구조를 통해 액체 방울이나 특정한 자기조립체로 조직화가 가능하다. 또 종횡비와 표면 양친매성의 조절을 통해 곡면, 주름, 원통형 등의 구조를 선택하고 ... ...

- [의학사로 읽는 세상] 뉴턴, 페스트 유행 기간 '만유인력의 법칙' 떠올렸다2022.10.11
- 가산점을 주겠다고 했지만 점수 신청을 한 학생은 거의 없었다. 신청을 한 극소수의 학생들도 점수에 눈이 먼 것인지 몇 줄 되지 않는 아이디어만 제시했을 뿐 이 아이디어의 진위를 확인하기 위한 기초적인 방법조차 제시하지 않았다. “지구상에 존재하는 모래는 모두 몇 개인가.” 이런 질문을 ... ...

- 소수의 트위터 사용자가 정치적 편견 만든다동아사이언스 l2022.10.03
- 연구 결과가 국제학술지 '사이언스 어드밴시스' 9월 30일자에 발표했다. 게티이미지뱅크 소수의 트위터 사용자가 정치적 성향에 관한 트윗을 공유하며 편견을 만들어낸다는 연구 결과가 나왔다. 소셜 미디어 플랫폼이 점차 많은 사람들에게 정치 정보를 제공하는 출처로 사용되지만 대다수의 트위터 ... ...

- 와인 성분으로 모발 이식용 접착제 만들었다동아사이언스 l2022.09.21
- 마치 비누 거품처럼 '미셀구조'를 만든다. 미셀 구조는 수용액 안에서 물에 녹지 않는 소수성 부분이 뭉쳐 동그란 모양을 형성하는 것을 말한다. 형성된 미셀 구조는 PEG가 감싸게 된다. 연구팀은 "마치 공들이 쌓여있는 것처럼 탄성을 띠어 고체처럼 움직인다"고 설명했다. 여기에 탄닌산을 ... ...
이전151617181920212223 다음

















