뉴스
"위아래"(으)로 총 1,774건 검색되었습니다.

- 스마트폰 끼고 사는 당신, 목디스크 위험동아일보 l2014.01.27
- [동아일보] 근육통 ‘담’과 달리 잠복기간 길어… 목뼈-관절 이상땐 완치 힘들어 스트레칭으로 어깨근육 풀어줘야 하루 24시간 중 고개를 숙인 시간을 헤아려 보면 몇 시간쯤 될까. 누워서 자는 시간, 소파에 기대 텔레비전 보는 시간 등을 빼면 목을 일자로 만드는 경우는 거의 없다. 대개 컴퓨터 ... ...

- 1000원이 1000엔보다 강하다고? 동아사이언스 l2014.01.24
- 측정되고 있다. 지폐 조각을 세로로 세워 위아래를 고정한 뒤, 압력을 가해 위아래를 당겨서 찢어지는 순간의 힘을 알아보는 것이다. 실험에 사용된 1000원짜리 지폐는 5.5kgf(킬로그램중·1kgf는 1kg에 작용하는 중력의 크기)의 힘이 가해지자 찢어졌다. 폭 1.5cm짜리 1000원짜리 지폐 조각으로 약 5.4kg(1 ... ...

- ‘나노횃불’로 생체현상 밝힌다동아사이언스 l2014.01.23
- 연세대 제공 국내 연구진이 기존 광학 현미경의 한계를 뛰어넘어 바이러스나 단백질을 자세히 관찰할 수 있는 기술을 개발했다. 연세대 김동현 전기전자공학과 교수와 최종률 박사팀은 빛이 자신보다 작은 구멍을 지날 때 발생하는 ‘나노횃불’로 단백질을 관찰하는 데 성공했다고 23일 ... ...
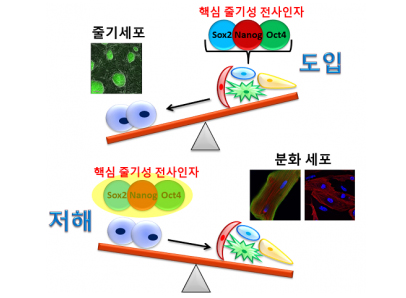
- 줄기세포로 암 뿌리째 뽑는다동아사이언스 l2014.01.20
- 분화가 끝난 체세포도 핵심전사인자를 넣으면 줄기세포가 될 수 있고(그림 위), 반대로 줄기세포라도 전사인자의 활성을 저해하면 분화가 촉진된다(그림 아래). - 성균관대 의과대학 제공 국제공동연구진이 줄기세포를 원하는 세포로 분화시키는 효율을 높일 수 있는 기술을 개발해 화제다. ... ...

- 철새 V자 대형의 비밀은 '상승기류'동아사이언스 l2014.01.19
- 붉은 부리의 새들이 일렬로 날갯짓을 하고 있다. 어떤 새는 날개를 위로 뻗고, 어떤 새는 날개를 구부리며 리듬을 타고 있다. 이번 주 ‘네이처’ 표지는 붉은볼따오기들이 차지했다. 스티븐 포르투갈 영국 왕립수의대 박사 연구팀이 철새가 V자 대형을 이루며 비행하는 것은 앞의 동료 철 ... ...

- 제작에서 경기까지… 로봇 영재들의 즐거운 하루동아사이언스 l2014.01.17
- 위이이잉-. 다리 8개를 재빠르게 움직이던 보행로봇이 집게팔로 공을 집어 올린다. 조정하던 참가자들은 이내 환호성을 질러댄다. 한편 급하게 후진하던 로봇이 공을 떨어뜨리자 어딘가에서 탄식이 이어진다. 지난 12월 28일(토) 일산 킨텍스(KINTEX)에서 열린 2013 영재 창의과학 경진대회(이하 대회)의 ... ...

- [2014 새해 특집]게임보다 재밌게… 떡잎때 창의력 DNA 심어동아일보 l2014.01.08
- [동아일보] [세계의 ‘창조 발전소’를 가다]핀란드 예술 교육기관 ‘안난탈로’ 사우나와 산타클로스의 나라 핀란드. 북유럽 핀란드의 다른 수식어는 교육 강국이다. 핀란드는 경제협력개발기구(OECD) 회원국의 15세 이상 학생을 대상으로 실시하는 국제학업성취도평가에서 1위를 단골로 차지하 ... ...
- 셰일가스 혁명 美, 세계 에너지시장 흔든다동아일보 l2014.01.03
- [동아일보] 일부 석유제품 반값 공세… 한국 등 아시아 정유사들 초긴장 세계 최대의 에너지 소비국인 미국이 ‘셰일가스 혁명’을 등에 업고 벌써 세계 에너지 시장을 쥐락펴락하고 있다. 액화석유가스(LPG) 등 석유 관련 제품의 생산비를 크게 낮춘 가격 경쟁력을 앞세워 공략에 나서면서 세계 정 ... ...

- 부정교합, 7세때 검사 받고 12세 전후 교정 받아야동아일보 l2013.12.30
- [동아일보] 위-아래턱 제대로 맞물리지 않는 부정교합… 언제 치료해야 좋을까 겨울방학을 맞은 학부모들의 고민거리 하나. “아이 턱 교정을 할까, 말까?” 위턱과 아래턱이 제대로 맞물리지 않는 ‘부정교합’은 일찍 치료할수록 좋다. 하지만 아이들의 턱 선은 대체로 완만하다. 잘 관찰하지 않 ... ...

- 피타고라스의 정리? 그림 한 장이면 OK!수학동아 l2013.12.17
- ‘피타고라스의 정리’는 직각삼각형에서 빗변을 제외한 나머지 두 변의 제곱의 합이 빗변의 제곱과 같다는 성질로, 수학을 잘 모르는 사람도 잘 아는 대표적인 수학 정리 중 하나다. 그런데 피타고라스의 정리를 만약 증명해 보라고 한다면? 정리를 아는 것과 증명을 하는 것은 또 다른 문제다. ... ...
이전164165166167168169170171172 다음

















